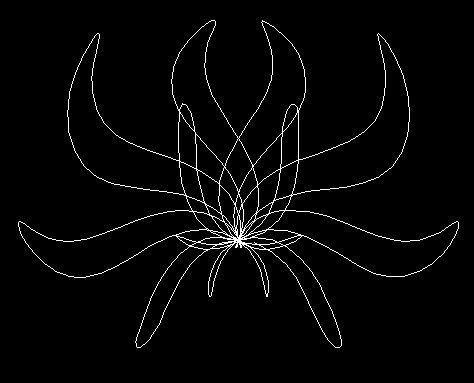
FOR theta = 0 TO 2 * pi STEP .015
rad = -(.5 * SIN(5 * theta)) * (.5 * COS(4 * theta)) * 1000
angle = theta + SIN(rad / 100)
xp = 320 + rad * COS(angle)
yp = 240 + rad * SIN(angle)
LINE -(xp, yp)
NEXT theta
Back when I was in school, and didn't have a workshop as a creative outlet, or a programming job to use up all of my algorithmic neurons, I did some programming just for fun. Although I wrote lots of little programs to solve various algorithmic and statistic problems, Simple and visually the coolest was a little program I wrote that used transcendental functions to draw various flowers and other visually appealing patterns.

|
Flower 1
FOR theta = 0 TO 2 * pi STEP .015 rad = -(.5 * SIN(5 * theta)) * (.5 * COS(4 * theta)) * 1000 angle = theta + SIN(rad / 100) xp = 320 + rad * COS(angle) yp = 240 + rad * SIN(angle) LINE -(xp, yp) NEXT theta |

|
Flower 2
FOR theta = 0 TO 4 * 3.1415 STEP .04 rad = (1.05 + SIN(theta * 4.5)) * 100 angle = theta - COS(theta * 10) / 10 xp = 320 + rad * COS(angle) yp = 240 + rad * SIN(angle) LINE -(xp, yp) NEXT theta |

|
Slinky
FOR theta = 0 TO 2 * 3.1415 STEP .02 xp = 320 + SIN(theta * 5) * COS(theta * 6) * 200 yp = 240 + COS(theta * 5.5) * SIN(theta * 6.5) * 200 LINE -(xp, yp) NEXT theta |

|
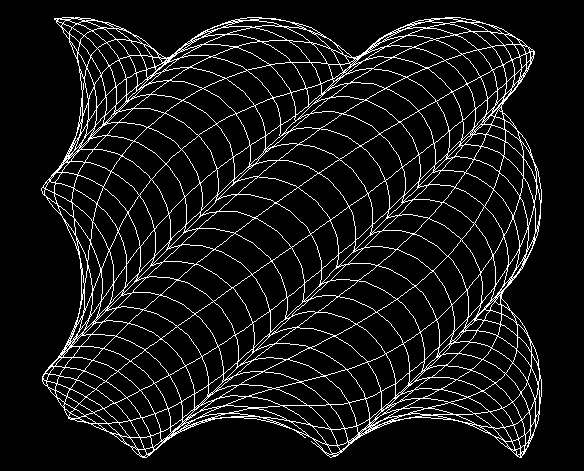
Shingles
FOR theta = 0 TO 160 STEP .06 xt = SIN(theta) * theta * 2 + 320 yt = COS(theta) * theta * 2 + 240 nthet = xt / 30 + yt / 30 othet = xt / 30 - yt / 30 yp = yt + SIN(nthet) * 15 + SIN(othet) * 15 xp = xt + COS(nthet) * 15 + COS(othet) * 15 LINE -(xp, yp) NEXT theta |
|
Waves
FOR theta = 0 TO 4 * 3.1415 STEP .004 xt = SIN(theta * 10) * 230 + 320 yt = COS(theta * 9.5) * 200 + 240 nthet = xt / 30 + yt / 30 yp = yt + SIN(nthet) * 20 xp = xt + COS(nthet) * 20 LINE -(xp, yp) NEXT theta |
Full Microsoft Quick Basic 4.5 Source Code for the whole program that I used to generate these patterns, plus some patterns that don't look as good.